Every bundle counts - A recipe for bundle-wise, myelin-weighted connectomes
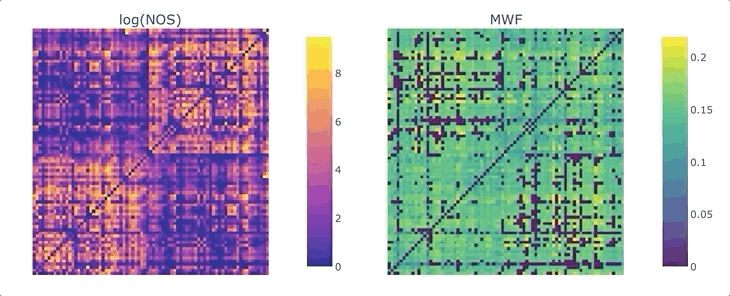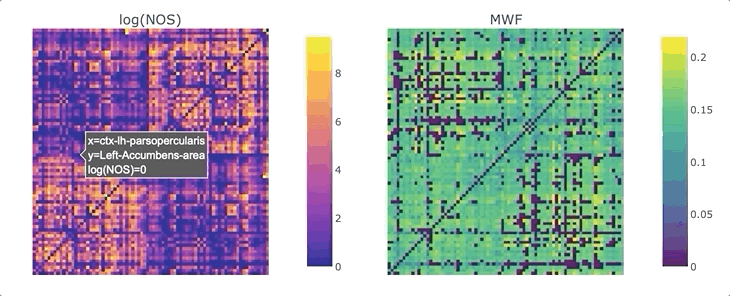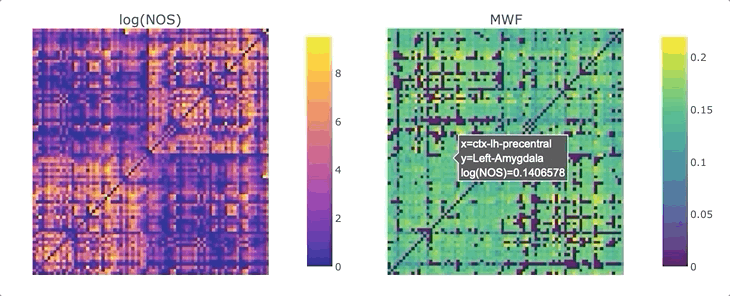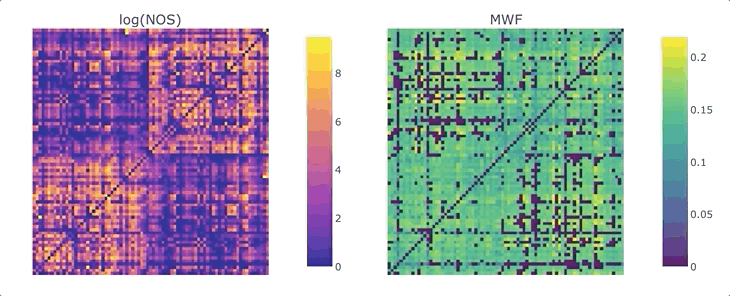
Esoteric connectomes
Graphs are straightforward objects: you have a bunch of nodes, some of them are inter-connected by edges, and it all makes sense. It is in real-world networks that things become complicated: what’s a node? What’s an edge? When it comes to the brain, the answers to these questions depend on what scale one is targeting, and what tools has available. For whole-brain, structural connectivity, the usual approach is to use tractography, and then count how many streamlines there are between each pair of regions to weight the associated graph. Number of streamlines (NOS) is not great, but it has been showed to somehow correlate with the microscopical fiber count. But what if we want to use something else as a weight? There’s a whole list of complementary MRI measures that could be use to provide complementary information. Most tools to make this fusion are available in MRtrix3, except maybe the last tricky one: averaging. It would be tempting to average each measure for each streamline, and then average again over the streamlines inter-connecting two areas - but this approach can introduce a NOS bias in the measure of interest. What if we want to compute, for each connection, the average across the whole bundle?
In this post, I will show the whole workflow of how to make one of these esoteric connectomes, from the pre-processing to the final bundle-wise averaging, using as a weight a myeline measure. All the related scripts are on the NeuroSnippets repository.
We want a matrix - squish those data!
We need a lot of stuff (parcellated anatomical data, pre-processed diffusion data, a myelin map) before getting to the actual issue we want to tackle, so we better get going. Publicly available myelin maps are not easy to find, but we are in luck as recently Kristin Koller and colleagues shared the MICRA dataset, containing a rich collection of data that is perfect for this scenario. Let’s start with downloading the data from OSF and the fundamental pre-processing: my usual choice for processing and parcellating T1-weighted data is FreeSurfer, but in this case to save time we will rely on FastSurfer. For the diffusion MRI pre-processing, we will use the papermill workflow I talked about last month. Once we have done all of that, we can actually start thinking about the core processing. Here is how these first steps look like:
# Downloading anatomical, diffusion and MWF data for subject 1 and session 1
wget https://files.osf.io/v1/resources/z3mkn/providers/owncloud/sub-01/ses-01/anat/sub-01_ses-01_T1w.nii.gz
wget https://files.osf.io/v1/resources/z3mkn/providers/owncloud/sub-01/ses-01/dwi/sub-01_ses-01_part-mag_dwi.nii.gz
wget https://files.osf.io/v1/resources/z3mkn/providers/owncloud/sub-01/ses-01/dwi/sub-01_ses-01_part-mag_dwi.bvec
wget https://files.osf.io/v1/resources/z3mkn/providers/owncloud/sub-01/ses-01/dwi/sub-01_ses-01_part-mag_dwi.bval
wget https://files.osf.io/v1/resources/z3mkn/providers/owncloud/sub-01/ses-01/fmap/sub-01_ses-01_part-mag_epi.nii.gz
wget https://files.osf.io/v1/resources/z3mkn/providers/owncloud/sub-01/ses-01/fmap/sub-01_ses-01_part-mag_epi.bvec
wget https://files.osf.io/v1/resources/z3mkn/providers/owncloud/sub-01/ses-01/fmap/sub-01_ses-01_part-mag_epi.bval
wget https://files.osf.io/v1/resources/z3mkn/providers/owncloud/derivatives/sub-01/ses-01/McDespot/MWF1.nii.gz
# Clone FastSurfer repo, install requirments and run FastSurfer
git clone git clone https://github.com/Deep-MI/FastSurfer.git
pip3 install -r FastSurfer/requirements.txt
mkdir fastsurfer_subjects
./FastSurfer/run_fastsurfer.sh --t1 sub-01_ses-01_T1w.nii.gz --sid sub1 --sd fastsurfer_subjects --parallel --threads 4
# Run diffusion pre-processing (using a tailor notebook and papermill)
mkdir dwpreproc
cd dwpreproc
papermill ../../papermill-preproc/dwi_preproc.ipynb -p ap ../sub-01_ses-01_part-mag_dwi.nii.gz \
-p pa sub-01_ses-01_part-mag_epi.nii.gz -p main_dir "AP" results.ipynb
cd ..
# Run actual processing
mkdir processing
cd processing
../build_bundle_connectome.sh ../dwpreproc/eddy_corrected.nii.gz ../dwpreproc/eddy_corrected.eddy_rotated_bvecs \
../sub-01_ses-01_part-mag_dwi.bval ../fastsurfer_subjects sub1 ../MWF1.nii.gz ../
Let’s now dive inside the main script: from the pre-processed data, we want first to make everything aligned. In this case, we are in luck since the myelin water fraction (MWF) map provided in the MICRA dataset can be linearly registered to the anatomical volume. For aligning the anatomical volume with the diffusion MRI data, we will use the boundary-based registration technique. Once we have these transformations, it is a matter of applying them:
# converting data to MIF
mrconvert -fslgrad $bvec $bval $dwi dwi.mif
dwibiascorrect ants dwi.mif dwi_unbiased.mif
dwi2mask dwi_unbiased.mif mask.nii.gz
# computing a masked meanb0
dwiextract -bzero dwi.mif b0_vols.nii
mrmath b0_vols.nii mean meanb0.nii -axis 3
mrcalc meanb0.nii mask.nii.gz -mult b0_masked.nii
# registration
mri_convert --in_type mgz --out_type nii --out_orientation RAS ${sub_folder}/$fs/mri/brain.mgz brain.nii
mrconvert ${sub_folder}/$fs/mri/aparc+aseg.orig.mgz aparc+aseg.nii
fast -v brain.nii
flirt -in $mymap -ref brain.nii -dof 6 -out mymap_anat.nii.gz
flirt -in b0_masked.nii -ref brain.nii -dof 6 -omat dw2anat_init.mat
flirt -in b0_masked.nii -ref brain.nii -cost bbr -wmseg brain_pve_2.nii.gz -init dw2anat_init.mat -omat dw2anat.mat \
-dof 6 -schedule ${FSL_DIR}/etc/flirtsch/bbr.sch
transformconvert dw2anat.mat meanb0.nii brain.nii flirt_import dw2anat_mrtrix.txt
mrtransform -linear dw2anat_mrtrix.txt -inverse mymap_anat.nii.gz mymap_dw.mif
mrtransform -linear dw2anat_mrtrix.txt -inverse brain.nii brain_dw.mif
mrtransform -linear dw2anat_mrtrix.txt -inverse -interp nearest -template brain.nii aparc+aseg.nii aparc+aseg_dw.mif
labelconvert aparc+aseg_dw.mif ${FREESURFER_HOME}/FreeSurferColorLUT.txt ${script_path}/fs_85nodes.txt nodes.nii
The next step is reconstructing a fiber-orientation distribution and performing whole-brain tractography: we will do that using multi-tissue, multi-shell constrainted spherical deconvolution and anatomy-constrained tractography, both implemented in MRtrix3. Once we have the tractogram, we also need to map the MWF data to the streamlines:
# generating 5tt file, FOD and tracking
5ttgen fsl -nocrop -premasked brain_dw.mif 5tt.mif
dwi2response msmt_5tt dwi.mif 5tt.mif wm.txt gm.txt csf.txt
dwi2fod msmt_csd dwi.mif wm.txt wm.mif gm.txt gm.mif csf.txt csf.mif -mask mask.nii.gz
tckgen wm.mif track1M.tck -act 5tt.mif -backtrack -crop_at_gmwmi -seed_dynamic wm.mif -minlength 10 -maxlength 250 -angle 30 -select 1M
tcksample track1M.tck mymap_dw.mif mymap.csv
We are ready to generate a connectome based on the number of streamlines using tck2connectome. But what about the bundle-wise connectivity we want to achieve? To take care of that, we can use python. We will need two things:
- the mapping between MWF and the streamlines: we generated that in the previous step;
- the list of ROIs from our parcellation scheme that the streamlines are connecting - we can obtain it defining the
-out_assignmentparameter when callingtck2connectome.
We are ready for the last steps:
# generating connectome
tck2connectome -symmetric -zero_diagonal -out_assignments fibers_assignment.txt track1M.tck nodes.nii connectome.csv
# removing comments from csv and txt files
sed -i '/^#/d' mymap.csv
sed -i '/^#/d' fibers_assignment.txt
# generating map-bundle-weighted connectome
${script_path}/bundle_connectome.py fibers_assignment.txt mymap.csv --mean connectome_mymap.csv
Bundle them up!
To finally build our bundle-wise, myelin-weighted connectome, we need less than 50 lines of python code. Let’s start from importing the packages and defining a couple of functions:
import numpy as np
import sys
def usage():
# Shows the general usage
print('Usage: '+sys.argv[0]+' in_assignment_file in_weight_file operation out_matrix')
def process(data, action):
# Process the data using the related action from numpy
if action == "--mean":
result = np.mean(data)
elif action == "--median":
result = np.median(data)
return result
if len(sys.argv) < 4:
usage()
sys.exit(1)
assert sys.argv[3] in ['--mean', '--median'], \
f"Unknown operation: {sys.argv[3]}. Must be one of: --mean, --median"
The process() function gives us the chance to choose if we want to compute the mean or the median for each bundle, and it is easy to extend it in case one needs a different central measure.
For the core steps of this script, we will heavily take advantage of python:
- we will loop in parallel through the assignment and mapping files;
- for each line, we will build a sparse matrix, where for each row and column we assemble a list of all the related values from the mapping;
- as we want a symmetric matrix, we will need to fill just half of the row-column combinations;
- once we have the complete sparse matrix, we will build the related full matrix using our central measure of choice.
Let’s translate these steps in code:
sparsemat = {}
with open(sys.argv[1], 'r') as f, open(sys.argv[2], 'r') as w:
# loop in parallel over the two files
for pair, values in zip(f,w):
row, col = [int(p) for p in pair.split(' ')]
if row > col:
# symmetric connectivity
row, col = col, row
key = (row, col)
dist = [float(v) for v in values.split(' ') if not np.isnan(float(v))]
sparsemat.setdefault(key,[]).extend(dist)
n = np.max([*sparsemat.keys()])
fullmat = np.zeros((n, n))
for ix in range(n):
for jx in range(ix+1, n):
fullmat[ix, jx] = process(sparsemat.get((ix+1, jx+1), 0), sys.argv[3])
fullmat[jx, ix] = fullmat[ix, jx]
np.savetxt(sys.argv[4], fullmat)
And we are done!
